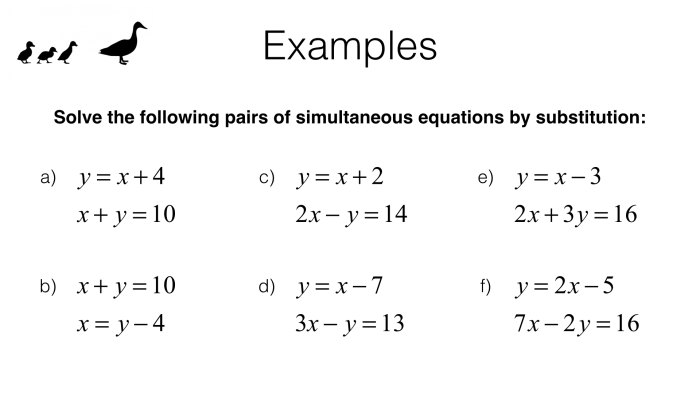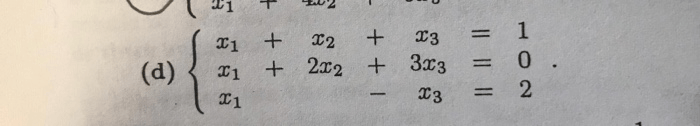The “Solving Systems of Linear Equations by Substitution Answer Key” provides a comprehensive resource for students seeking to master this fundamental algebraic technique. By presenting a clear and systematic approach, this guide empowers learners to confidently solve systems of equations and apply them to real-world problems.
Delving into the intricacies of the substitution method, this guide meticulously Artikels each step, enabling students to navigate the process with precision. Furthermore, it explores variations and applications of the method, fostering a deeper understanding of its versatility and utility.
Solving Systems of Linear Equations by Substitution: Solving Systems Of Linear Equations By Substitution Answer Key

The substitution method is a technique used to solve systems of linear equations by substituting one equation into another. This method involves isolating a variable in one equation and substituting its expression into the other equation, allowing you to solve for the remaining variable.
To use the substitution method, follow these steps:
- Solve one equation for one variable.
- Substitute the expression for that variable into the other equation.
- Solve the resulting equation for the remaining variable.
- Substitute the value of the second variable back into either of the original equations to solve for the first variable.
The substitution method is a straightforward and efficient approach to solving systems of linear equations, especially when one of the variables can be easily isolated.
Examples of Solving Systems of Linear Equations by Substitution
Example 1: Solve the system of equations:
- x + y = 5
- x – y = 1
Solution:
- Solve the first equation for x: x = 5
y
- Substitute x = 5
y into the second equation
(5
- y)
- y = 1
- Solve for y: y = 2
- Substitute y = 2 back into the first equation to solve for x: x + 2 = 5
- Solve for x: x = 3
Therefore, the solution to the system is (x, y) = (3, 2).
Applications of Solving Systems of Linear Equations by Substitution
Solving systems of linear equations by substitution has numerous applications in various fields:
- Science:Modeling physical phenomena, such as motion, heat transfer, and chemical reactions.
- Engineering:Designing structures, optimizing circuits, and solving fluid flow problems.
- Economics:Analyzing market equilibrium, forecasting demand, and optimizing production.
For example, in economics, systems of linear equations can be used to determine the optimal quantity of goods to produce and the prices to charge in order to maximize profit.
Variations of the Substitution Method
The substitution method can be modified to handle more complex systems of equations:
- Elimination method:Involves adding or subtracting multiples of one equation to another to eliminate a variable.
The choice of method depends on the specific system of equations and the ease of isolating variables.
Using Technology to Solve Systems of Linear Equations, Solving systems of linear equations by substitution answer key
Technology can be used to solve systems of linear equations efficiently:
- Graphing calculators:Can plot equations and find their intersection points.
- Software programs:Such as MATLAB or Mathematica, can solve systems of equations symbolically or numerically.
Using technology can save time and reduce the risk of errors, but it is still important to understand the underlying concepts of the substitution method.
Top FAQs
What are the advantages of using the substitution method?
The substitution method is advantageous when one variable can be easily isolated and substituted into the other equation, simplifying the system.
Can the substitution method be used to solve all systems of linear equations?
No, the substitution method is not suitable for systems where both variables cannot be easily isolated.
What are some real-world applications of solving systems of linear equations?
Solving systems of linear equations has applications in fields such as engineering, economics, and physics, where it is used to model and solve complex problems involving multiple variables.